#Avoiding decades of unstable fluid singularities by scientists, DeepMind has found them using AI

The invisible singularity hidden in the fluid for decades has finally been found——

AI has made great contributions.

Google DeepMind, in collaboration with Brown University, New York University, and Stanford University, used a combination of Physics Informed Neural Network (PINN) and high-precision numerical optimization to identify unstable singularities in fluid equations.

It is said that this kind of singularity is very “picky”, disappearing as soon as the initial conditions are almost the same. It was never found before, but this time it was discovered by AI.

Let’s take a closer look below.

##Combination punch of AI+high-precision calculation

Let’s first talk about why unstable singularities are difficult to find.

What is a singularity? Simply put, in mathematical equations of fluid motion (such as equations describing water flow and airflow), previously smooth solutions may suddenly exhibit an infinite magnitude, such as an infinite velocity gradient.

This may seem impossible in physics, but mathematically it has not been clear whether this situation can really happen, especially in fluids without boundaries (such as open water flows), which is a super difficult mathematical problem.

Previously, most of the singularities found by scientists were stable. Even if the initial conditions change slightly, this singularity will still appear, which is easier to capture.

But everyone speculates that singularities like the boundaryless 3D Euler equation and Navier Stokes equation (one of the six millennium problems in mathematics) should be unstable.

This kind of unstable singularity is very picky, and the initial conditions must be precise enough that they cannot be any more precise. As long as there is a slight deviation, the singularity will not appear, so it was impossible to find it using traditional numerical methods before.

But this time, researchers have developed a new computational framework and finally systematically identified such unstable singularities.

Through the technical path of Physics Informed Neural Network (PINN) and high-precision numerical optimization, we have successfully located unstable singularities in fluid motion equations that were previously difficult to capture. This achievement also provides a new paradigm for the study of nonlinear fluid dynamics.

The focus of this study is on unstable singularities, which belong to the category of * * non regular singularities * *. The biggest feature is that the Lyapunov exponent of the initial disturbance (which can be simply understood as a small initial difference that increases over time) is extremely high.

Even small initial parameter deviations, such as velocity gradients and pressure field distribution errors, can be amplified by the nonlinear terms of the equation, leading to the annihilation of singularities in traditional numerical calculations.

In the past, when researchers used traditional numerical methods such as finite element method and finite difference method to solve problems, they were limited by the accuracy of mesh discretization and computational convergence, and were unable to lock the stable existence region of such singularities in phase space.

The key to achieving a breakthrough this time lies in the construction of a dual layer computing framework consisting of AI pre search and high-precision optimization.

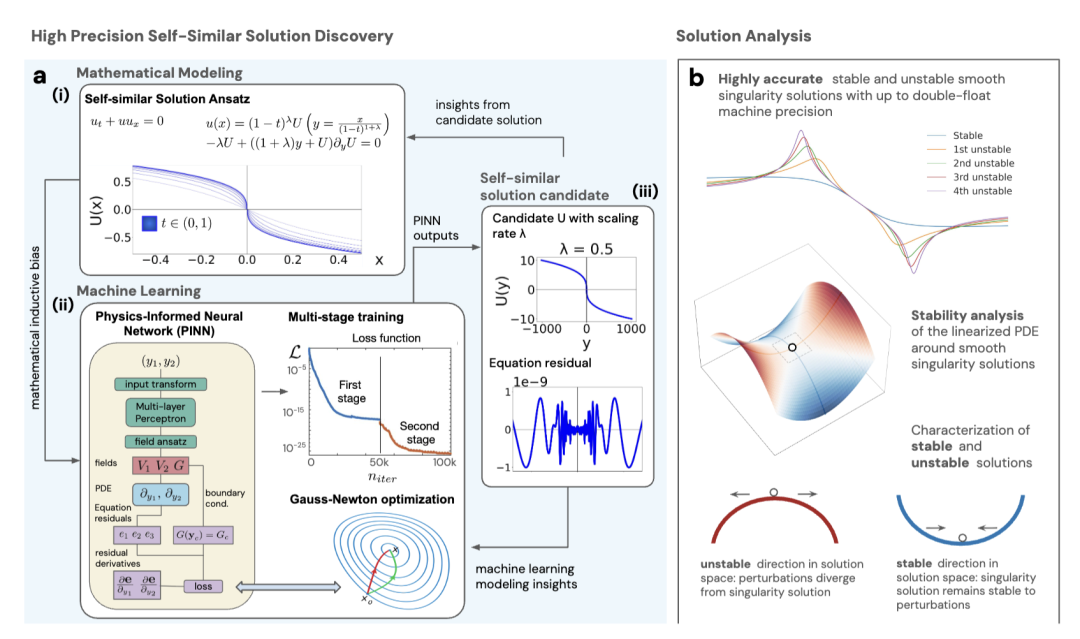
In the first stage, the research team constructed a prediction model based on a Physics Informed Neural Network (PINN), embedding the control equation of the Navier Stokes equation as a regularization term into the network loss function. The model was trained using gradient descent algorithm to learn the nonlinear evolution law of the flow field, quickly surrounding the possible attractor regions of singularities in high-dimensional phase space, greatly reducing the search range.

In the second stage, the team introduced the Gaussian Newton optimizer and Levenberg Marquardt algorithm to perform high-precision numerical correction on the candidate regions output by PINN.

At the same time, combined with Bayesian optimization dynamic adjustment, we successfully captured * * 3 unstable singularities that satisfy Hopf bifurcation conditions in the atmospheric boundary layer flow equation, and locked in * * the fourth candidate singularity * * through eigenvalue analysis;

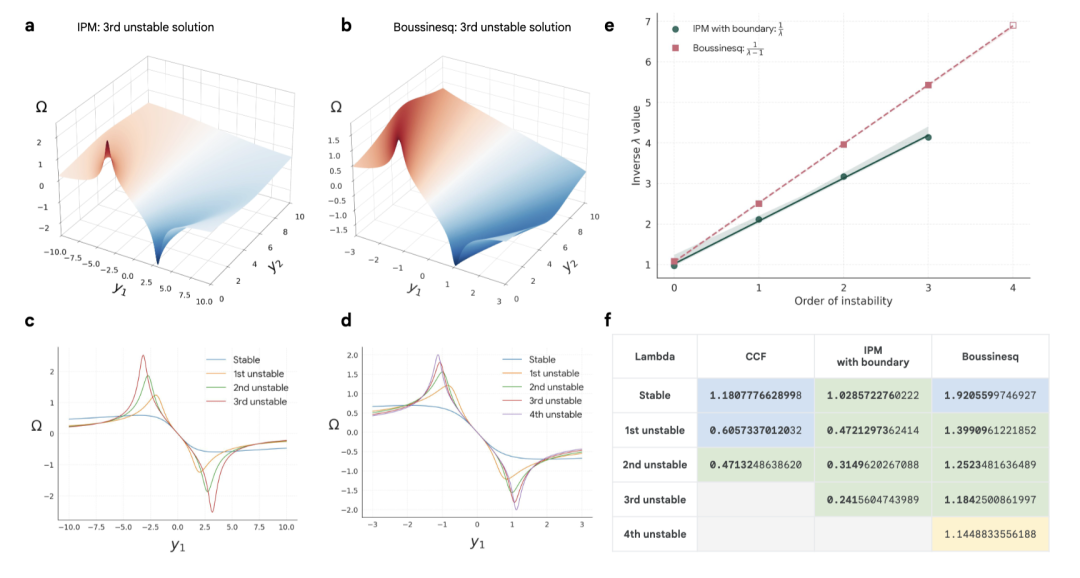
In the Darcy Brinkman equation for porous media flow (fluid passing through rock/soil), in addition to one stable saddle point singularity, three previously unreported hidden singularities were identified. The existence of these singularities explains the local abrupt mechanism of non Darcy flow phenomena in porous media.

More groundbreaking is that the research team derived an analytical formula for the runaway velocity of the nth singularity based on its topological characteristics and evolution speed, providing a clear theoretical basis for subsequent singularity searches.

For popular scenarios, the significance of this study may lie in:

+Predicting typhoons: more accurately capturing sudden changes in typhoon paths to avoid forecast bias;

+Improved aircraft: More accurate calculation of airflow resistance to the fuselage, making the aircraft more fuel-efficient.

It can be seen that AI technology has become a powerful assistant to traditional scientific research.

*Paper address: https://arxiv.org/abs/2509.14185 *

Reference link: *[1] https://deepmind.google/discover/blog/discovering-new-solutions-to-century-old-problems-in-fluid-dynamics/ *
*[2] https://x.com/GoogleDeepMind/status/1968691852678173044 *